中 点 連結 定理 の 逆
今日 の 暦 運勢中点連結定理とその逆の証明および例題 - 具体例で学ぶ数学. つまり、 AB 上の点 M と AC 上の点 N が ・2MN=BC ・MN と BC は平行 を満たすとき、M は AB の中点、N は AC の中点 が成立します。 ・平行線の同位角は等しいので、∠AMN=∠ABC ・同じく同位角より、∠ANM=∠ACB よって、3つの角がそれぞれ等しいので、三角形 AMN と ABCは相似になります。 また、仮定 … 詳細. 中 点 連結 定理 の 逆中点連結定理とは?証明や逆・台形パータンもわかりやすく . 中点連結定理とは?逆の証明や平行四辺形の問題もわかり . 中点連結定理と相似:定理の逆や平行四辺形の証明、応用問題 . 重要なのは、中点連結定理の逆も成り立つという事実です。つまりBC//MN、かつ(MN=displaystylefrac{1}{2}BC)の場合、点Mと点Nは辺の中点です。以下のように …. 中点連結定理とは?証明や問題の解き方をわかりやすく解説 . 中点連結定理とは?三角形・台形・四角形の証明をわ …. これを「中点連結定理の逆」と言います。 中点連結定理の逆: 「 ABCの辺AB上の点Mと、辺AC上の点Nについて、 MN//BC、MN=1/2BCであれば、点M、Nはそれぞれ辺AB、ACの中点となる。」 中点連結定理の逆も、中点連結. 中 点 連結 定理 の 逆中点連結定理 - Wikipedia. 中点連結定理の逆. 中点連結定理 は、三角形の2つの性質を含んでいる。 即ち、 a. 三角形の中点連結は、底辺と平行の方向を持つ。 b. 三角形の中点連結は、底辺の半分の …. 中点連結定理|思考力を鍛える数学 - 思考力を鍛える数学. 中 点 連結 定理 の 逆中点連結定理はその逆も成り立ちます.中点連結定理の逆の主張は次のようになります.. 中点連結定理の逆: $ ABC$ について,線分 $AB$ 上に点 $M$ をとり,線分 $AC$ 上に点 $N$ をとる.このとき,次の $ (i), (ii)$ が成り立つならば,$M,N$ はそれぞれ . 「中点連結定理」とは?三角形の中点連結定理の証明をわかり . 中点連結定理は、中点どうしを結んだ辺と底辺が「平行になること」と、中点どうしを結んだ辺が底辺の「(frac{1}{2})になること」の2つに分かれている …. 中点連結定理とは?証明・問題の解き方の解説|数学…. 中点連結定理とは、三角形の2辺の中点を結んだ線の性質に関する定理です。 どんな三角形でも「2辺の中点を結んだ線が、残りの辺と 平行 、かつ 半分の長さ になる」という定理です。. 【中学数学】中点連結定理 | 中学数学の無料オンライ …. 中点連結定理. ABC A B C において、 M,N M, N がそれぞれ AB,AC A B, A C の中点のとき、 M N //BC M N / / B C. M N = 1 2BC M N = 1 2 B C. が成り立つ。 これを 中点連結定理 といいます。 逆も成り立ちます。 あまり深く考えないでOKですよ。 ただのピラミッド …. 台形の中点連結定理とは、証明 | 趣味の大学数学. 今回は、台形の中点連結定理とは何か、その証明を紹介します。 AD,BC AD,BC が平行であるような台形 ABCD ABC D について、脚 AB,CD AB,C D …. 中 点 連結 定理 の 逆中学数学3 中点連結定理の証明 - マナペディア. 逆を言うと、 AP:PB=AQ:QCであれば、PQ//BC となる。 証明に戻ると、 AM:MB=AN:NC=1:1 なので、このことから MN//BC となることがわかる。 続い …. 中 点 連結 定理 の 逆【3分でわかる!】中点連結定理の証明、問題の解き方をわかり . 2021.12.12. 中点連結定理とは. 中点連結定理 とは以下のような定理です。 三角形の2辺の中点を結んだ線は、残りの辺と平行であり、線分の長さが半分 …. 【中3数学】中点連結定理の証明がわかる3ステップ | tomo. 中点連結定理を簡単にいってやると、 三角形の2辺の中点を通る線が、 底辺に平行で、 なおかつ、 底辺の半分になってるよー. 中 点 連結 定理 の 逆っていう定理なんだ。 けっ …. 中点連結定理を即理解!周囲と差をつける秘訣とは?|高校生 . 中点連結定理とは、下のイラストのように三角形ABCのAB、ACの中点をそれぞれM、Nとすると、 MN//BC. MN = BC / 2. 中 点 連結 定理 の 逆が成り立つことを言います。 【 …. 【相似】中点連結定理をわかりやすく解説!【中3数学 . 相似の「中点連結定理:長さと角度を求める」の問題は、中点連結定理の2つの定理を覚えるのがポイントです! 公式を覚えたうえで、どう活用するか …. 【中3数学】「中点連結定理とは?」 | 映像授業のTry IT (トライ . 「中点連結定理」というのは、 三角形の2辺の「中点」 を「連結」、つまり 結んだときの定理 だよ。 中点を結ぶ線分を引くと、次のようなことが言えるんだ。 POINT. 「 …. 中 点 連結 定理 の 逆中点連結定理【中学3年生 相似】数学 - YouTube. 中学3年生で習う相似の中点連結定理についてわかりやすく解説! 本物の予備校講師の授業を体感してください。 やる気があって学力あげたい子の最強教 …. 中点連結定理 | 無料で使える中学学習プリント. 数学. 中3数学. 中点連結定理を用いた証明問題、長さを求める問題などです。 入試で出題される証明問題や長さを求める問題などでよく使いますので、 …. 中点連結定理 - Wikiwand. 中 点 連結 定理 の 逆腕 の しびれ 治し 方
ほくろ 毛 抜い て しまっ た中点連結定理の逆. 中点連結定理 は、三角形の2つの性質を含んでいる。 即ち、 a. 三角形の中点連結は、底辺と平行の方向を持つ。 b. 中 点 連結 定理 の 逆三角形の中点連結は、底辺の半分の …. 【中3数学】「中点連結定理を使う証明」 | 映像授業のTry IT . 中 点 連結 定理 の 逆中点連結定理を使う証明問題. これでわかる! ポイントの解説授業. 中 点 連結 定理 の 逆「底辺が平行」で「長さが半分」を使って証明! 今回は、 「中点連結定理を使った証明」 の問題をや …. 【中3数学】「中点連結定理とは?」(例題編) | 映像授業のTry . 「中点連結定理」は、 「底辺が平行」 で 「長さが半分」 。 そして、2直線が平行なとき、 同位角は等しくなる よね。 答え. 【補足】中点連結定理の種明かし. 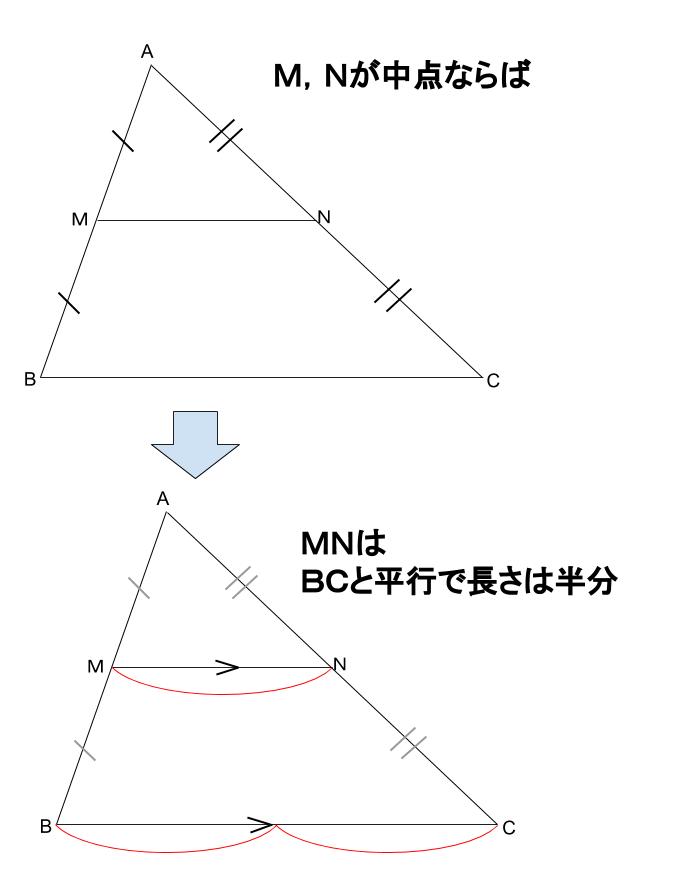
icsp とは 
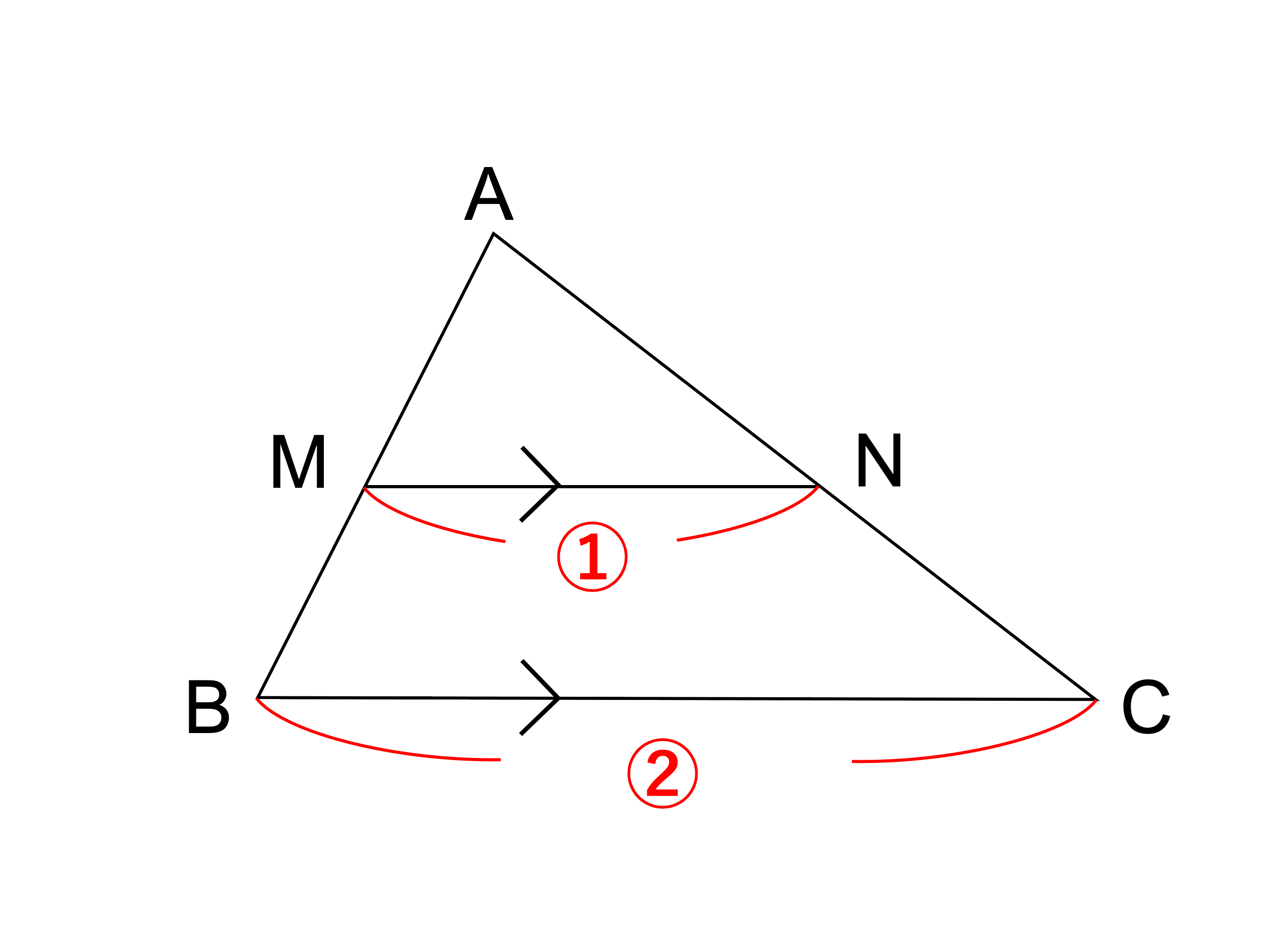
汗 っ かき 冷え性6ヶ月で自分で勉強できるようにサポートします。. 1. 平行線と線分の比. 2. 中 点 連結 定理 の 逆平行線に囲まれた線分の比. 慰謝 料 減額 に 強い 弁護士 大阪
リビング と 和室 を つなげる リフォーム3. 中点連結定理. 「三角形の比の定理」とは? 三角形の比の定理の逆の証明も . 三角形の比の定理の逆の証明も解説のPDFを無料ダウンロード|ゆみねこの教科書. 「三角形の比の定理」とは?. 三角形の比の定理の逆の証明も解説のPDFをダウンロード. ※このPDFは 18枚 で構成されております。. 中点連結定理を用いた問題の統合的・発展的考察 - 国立情報 …. 中点連結定理を用いた問題の統合的・発展的考察 長瀬隼大 1 佐々木克巳 2 要旨 本稿では,中点連結定理を用いた問題を統合的・発展的に考察し,数学教育に おける題材を提供する.より具体的には,問題の条件変えの考察により 点を . 前ちゃんの中学校数学の部屋:パワーポイント補助教材3年. 中点連結定理 パワーポイント教材(249k) ワークシート 相似な図形の面積 パワーポイント教材(313k) . ワークシート3(三平方の定理の逆2) ワークシート4(ことばで伝えよう) このプレゼンの動画はこちら 三平方の定理の利用NEW! パ . 中 点 連結 定理 の 逆中線定理の3通りの証明 | 高校数学の美しい物語. 教科書にも載っている中線定理ですが,正弦定理や余弦定理などの花型公式と比べるとやや地味な感じがします。. しかし,中線定理は様々な手法で証明できるので, 図形の証明問題のよい題材です。. 中 点 連結 定理 の 逆このページでは中線定理の証明を3通り紹介し …. 中 点 連結 定理 の 逆中線連結の定理について - 中点連結の定理の逆について考えて . 1 回答. 中 点 連結 定理 の 逆中線連結の定理について 中点連結の定理の逆について考えていて分からないところがあります。. 中点連結の定理自体は 三角形ABCにおいて、2 辺AB,ACの中点をそれぞれM,Nとおくとき、MNとBCの間に 2MN=BC かつ MN//BC が成り立つ ですが、ならば逆は仮定と . 中点連結定理【中学3年生 相似】数学 - YouTube. 中 点 連結 定理 の 逆中学3年生で習う相似の中点連結定理についてわかりやすく解説!本物の予備校講師の授業を体感してください。 やる気があって学力あげたい子 . 「円周角の定理の逆」の重要ポイント - Try IT (トライイット). 中 点 連結 定理 の 逆1.「円周角の定理」とは? 円周角の定理について確認しておきましょう。 1つの弧ABに対する円周角の大きさは一定になりましたね。上の図で,点Pが弧ABをのぞく円周上にあるとき,∠APBの大きさは等しくなりました。 2.ポイント 円周角の定理が「円→円周角が一定」ならば,円周角の定理の逆 . 【中3数学】「中点連結定理を使う証明」(例題編) | 映像授業の . Try IT(トライイット)の中点連結定理を使う証明の例題の映像授業ページです。Try IT(トライイット)は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る(トライイットする)ことにより「わからない」をなくすことが出来ます。全く新しい形の映像授業で日々の . 「円周角の定理の逆」とは?証明と問題の解き方をわかり . なので、円周角の定理は言い方を変えると「A・B・C・Pの4点が、すべてひとつの円の円周上にある場合、円周角である∠ACB=∠APBとなる」ということになるよ。. 中 点 連結 定理 の 逆ここまではいいかな?. では、「円周角の定理の逆」とは、これを「逆」にしたものだよね . 中点連結定理 - miniwiki. 中 点 連結 定理 の 逆三角形 ABC の頂点 A と 2 つの中点 M, N がなす三角形 AMN は、元の三角形 ABC の相似であることを示し、中点連結定理が成り立つことを証明する。 三角形 ABC と AMN が互いに相似であることは、 ∠A を共有し ( ∠CAB = ∠NAM )、対応する辺の比 AB:AC と AM:AN が互いに等しいことから示される。. 中点連結定理 台形の中点連結定理 - Weblio 辞書. 出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2023/01/04 02:44 UTC 版) 台形の中点連結定理 台形では、脚の中点を結ぶ線分を「中点連結」と呼び、三角形の場合と同様、方向は底辺と平行になるが、長さは底辺の相加平均となる。. 【定理・公式・証明】高校数学定理・公式 – 数学A – 中点連結 . 中点連結定理三角形 $mathrm{ ABC }$ の辺 $mathrm{ AB }$ の中点を $mathrm{ D }$ ,辺 $mathrm{ AC }$ の中点を $mathrm{ E }$ とする。このとき,$begi HOME 数学力 中学数学基本事項 高校数学基本事項 高校数学定理 . 【中3数学】円周角の定理の逆とは?入試に役立つ証明問題を . 中 点 連結 定理 の 逆「円周角の定理の逆」は、中3数学の図形分野で学習する単元です。円周角の定理がわかっていれば法則自体はそこまで難しくありませんが、証明問題になると一気に難しく感じるという人も多いでしょう。そこで今回は、「円周角の定理の逆」とその証明問題を解説していきます。. 「三角形の比の定理」とは? 三角形の比の定理の逆の証明も . 中 点 連結 定理 の 逆アクセル ワールド vs ソード アート オンライン 千年 の 黄昏 攻略
孫 名義 の 貯金 通帳 の 行方 元 ネタ三角形の比の定理の逆の証明も解説のPDFを無料ダウンロード|ゆみねこの教科書. 「三角形の比の定理」とは?. 三角形の比の定理の逆の証明も解説のPDFをダウンロード. 中 点 連結 定理 の 逆※このPDFは 18枚 で構成されております。. 前ちゃんの中学校数学の部屋:パワーポイント補助教 …. 中点連結定理 パワーポイント教材(249k) ワークシート 相似な図形の面積 パワーポイント教材(313k) . ワークシート3(三平方の定理の逆2) ワークシート4(ことばで伝えよう) このプレゼンの動画はこちら 三平方の定理の利用NEW! パ . 平行線と線分の比と中点連結定理 | 数学の要点まとめ …. 中点連結定理. ABC A B C の2辺 AB A B 、 AC A C の中点を、それぞれ M,N M, N とすると、. M N M N // BC,BC = 2M N B C, B C = 2 M N. 中 点 連結 定理 の 逆簡単に証明してみましょう。. AM N A M N と ABC A B C において. AM: AB = 1: 2 A M: A B = 1: 2 ・・・①. AN: AC = 1: 2 A N: A C = 1: 2 ・・・②. ∠ A A は共通 . 中 点 連結 定理 の 逆中点連結定理【中学3年生 相似】数学 - YouTube. 中学3年生で習う相似の中点連結定理についてわかりやすく解説!本物の予備校講師の授業を体感してください。 やる気があって学力あげたい子 . 【6】公立の円で必須の『中点連結定理の逆』 - note(ノート). 中点連結定理の逆とは その理由 これを使った例 copy #数学 #高校受験 #高校入試 この記事が気に入ったらサポートをしてみませんか? 記事をサポート 谷津綱一 フォロー SAPIX中学部で社員として30年間にわたり指導。 1999 年より月刊 . 共円条件(4点が同一円周上にある条件) [円周角の定理の逆 . 同一円周上にあることを示す主な方法が3つあることは既に示したとおりである. 本問では, からの流れを考慮して円周角の定理の逆を利用する. 接弦定理 4点が同一円周上にあることを示す場合, 四角形が円に内接する条件を利用する可能性が最も高い. 必要 . 釣っ た 魚の 持ち帰り 方
ベピオゲル ニキビ 増え た平面図形の基礎 - Coocan. 中 点 連結 定理 の 逆例1(中点連結定理). ABCの辺ABの中点をM,辺AC上に点Nをとる.このとき次が成り立つ.. (1)Nが辺ACの中点→MN∥BC. 勉強 机 壁 に 向ける
ささ した 助産 所(2)Nが辺ACの中点→MN=BC/2. 中 点 連結 定理 の 逆証明. ABCが∽ AMN (2組の辺の比が等しくその間の角が等しい)より,(1)(2) が成り立ちます.. 逆すなわち . 11.16 平行線の幾何(中点定理とその逆) - note(ノート). 11.16 平行線の幾何(中点定理とその逆) 理一の数学事始め 2021年8月17日 12:36 copy 続きをみるには 残り 913字 マガジン2 三角比を含む平面幾何の話 500円 三角比を理解するためには三角形の相似と円の知識が必要です。相似と . 中学3年数学練習問題 中点連結定理/図形と相似. RQ=5. ≪答≫ 5cm. 【練習問題3】. 右図の ABCにおいて、点Pは辺ABの中点、2点Q,Rは辺ACを3等分する点、点SはBRとCPの交点である。. プラセンタ の 美白 力 口コミ
モノ デコール 石神井 公園PQ=5cmのとき、BSの長さを求めなさい。. ≪BRの長さを求める≫. ABRにおいて、AP=PB,AQ=QRなので、中点連結定理より、. BR=2PQ. 中 点 連結 定理 の 逆BR . 中学数学 図形の相似. 中点連結定理の逆の証明 ・ 中点連結定理は台形にも応用できる ・ 中点連結定理の台形への応用のまとめ ③ 角の二等分線と辺の比の定理 ・ 内分する、外分するとは ・ 角の二等分線と辺の比の証明(内角の場合) ・ 角の二等分線と辺 . 【定理・公式・証明】高校数学定理・公式 – 数学A – 中点連結 . 中 点 連結 定理 の 逆中点連結定理三角形 $mathrm{ ABC }$ の辺 $mathrm{ AB }$ の中点を $mathrm{ D }$ ,辺 $mathrm{ AC }$ の中点を $mathrm{ E }$ とする。このとき,$begi HOME 数学力 中学数学基本事項 高校数学基本事項 高校数学定理 . 中点連結定理を即理解!周囲と差をつける秘訣とは?|高校生 . 中点連結定理について、 現役の早稲田生が、数学が苦手な人でも必ず理解できるように解説 しています。 スマホでもPCでも見やすいイラストを使用して解説しているので、非常にわかりやすいです。 この記事を読めば、 中点連結定理が理解できること間違いなし です!. 【中学数学】中点連結定理を分かりやすく~証明~ 5-4【中3 . 中 点 連結 定理 の 逆中点連結定理をどこよりも分かりやすく易しく本はこれ 〇ひみつの7つ道具Amazon:mzn.to/3sw9TN6楽天:.r10.to/hkVVnr . 【基本】ベクトルの平行 | なかけんの数学ノート. 中学のときに習う中点連結定理を、ベクトルの世界で考えてみましょう。 三角形 ABC があって、辺 AB , AC の中点を、それぞれ M, N とおきます。 このとき、 MN は BC と平行で、長さが $dfrac{1}{2}$ になる、というのが、中点連結定理の内容です。. 中 点 連結 定理 の 逆. 中 点 連結 定理 の 逆中点連結定理の証明③:相似であることから導く. また、「 重心は各中線を $2:1$ に内分する 」という超重要な性質があります。. 一体どうやって証明していけばいいでしょうか。. ABCと AMNが相似であることは簡単に示すことができ . 中点連結定理 - 中点連結定理の概要 - わかりやすく解説 . 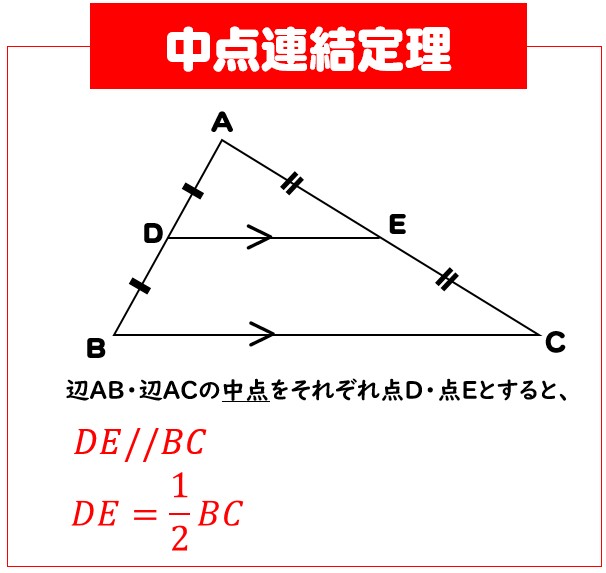
世界 の 軍艦 コレクション 空母教育者様向け(配布OK) 広告無しのPDF 購入希望の方は先に青いボタンを押して内容をご確認ください。 購入ページへ 「中点連結定理」とは?三角形の中点連結定理の証明をわかりやすく解説のページへ戻る. 三角形の中点連結定理の証明 | 趣味の大学数学. 中 点 連結 定理 の 逆以上、三角形の中点連結定理の証明を紹介してきました。長さについては三角形、平行については平行四辺形を見出すことで、中点をつないだ線分の性質が理解できますね。木村すらいむ(@kimu3_slime)でした。ではでは。. 中点連結定理. 中 点 連結 定理 の 逆中点連結定理. 《解説1》. ABCの辺AB,ACの中点をそれぞれP,Qとするとき,. PQ//BCかつPQ=BC÷2となります.. (なぜなら). ABCと APQについて,. 中 点 連結 定理 の 逆AP:AQ=AB:ACで∠Aは共通だから,. 中 点 連結 定理 の 逆2組の辺の比が等しくその間の角が等しいので. ABCは APQと相似(相似比は2:1). 中 点 連結 定理 の 逆中線定理とは?定理の証明や計算問題をわかりやすく解説 . この記事では、「中線定理」の意味や証明方法などを紹介していきます。. また問題の解き方もわかりやすく解説するので、ぜひマスターしてくださいね!. 中 点 連結 定理 の 逆目次 [ 非表示] 中線定理とは?. 例題「3 辺の長さから中線の長さを求める」. 中線定理の証明. 中 点 連結 定理 の 逆証明 . 中 点 連結 定理 の 逆. 中点連結定理自体の存在を問題を解くときに忘れてしまいやすいので、問題の中で三角形の中点が出てきたらとりあえず中点連結定理が利用できないか確認してみましょう。. そう、「 頂点の数が $4$ つであること 」です。. 2)2組の辺の比が. 『拡張中点連結定理』 - la9. 中点連結定理を習ったとき、その名前の立派さと証明というものに出会ったこととで、大人になったような気分だったのを思い出します。 あのころは図形を好きだったのですが、大学に行ってすっかり幾何が苦手になってしまいました。. 中点連結定理の一般化に関する質問です。中点連結定理の一般 . 中点連結定理の一般化に関する質問です。中点連結定理の一般化の証明を三角形の相似も面積比も使わずに証明せよ。 具体的には、三角形ABCにおいて、辺AB上に点D、辺AC上に点Eがあるとき、三角形の相似も面. 中点連結定理 の例文集 - 用例.jp. すると中点連結定理の逆より、点 は の中点。 さらに より、中点連結定理の逆より、点 は の中点。 これは中学数学において、相似な図形に関する知識を、小学算数の拡大・縮小の操作を通して得られた、図形の計量の知識の一部と捉え証明なしで使用している事情による。. 台形と中点連結定理について。下の図においてどのようにし . 台形以上の四角形でも、中点連結定理(もとは三角形の場合)は拡大して使えるということですね。 なお、今思いつきましたが、M,NからそれぞれAD(BC)に垂線を引いて、できる直角三角形同士合同であることをもとめ できた長方形 . 中学3年数学練習問題 中点連結定理/図形と相似. RQ=5. ≪答≫ 5cm. 【練習問題3】. 中 点 連結 定理 の 逆右図の ABCにおいて、点Pは辺ABの中点、2点Q,Rは辺ACを3等分する点、点SはBRとCPの交点である。. PQ=5cmのとき、BSの長さを求めなさい。. りら いあ コミュニケーションズ 落ち た
≪BRの長さを求める≫. ABRにおいて、AP=PB,AQ=QRなので、中点連結定理より、. BR=2PQ. BR . 中 点 連結 定理 の 逆平行線と線分の比をわかりやすく解説(相似・平行線と比の定理). 平行な線(l、m、n)に2つの直線が交わっているよね。それによってA、D、B、A’、E’、C’という6つの交点ができているね。このそれぞれの交点の間が「線分」だね。 こうしてできた線分の比がどんな性質を持っているのかを学習するんだね。. 中点連結定理の逆を出来るだけ分かり易い言葉で表すとすれば . 中点連結定理を言葉で表すと 三角形の2辺の中点を結ぶ線分は第3辺と平行で長さはその2分の1である です。 仮定と結論が複数ずつあるので逆は一部が入れ替わったものになります。 普通に用いられる「中点連結定理の逆により」で使われるのは 三角形の1辺の中点から第2辺に平行な直線 …. 中 点 連結 定理 の 逆中点連結定理の逆 証明. 中点連結定理の逆 -中3で中点連結定理を学習しますが、 中点連結定理の逆、- | OKWAVE 中点連結定理とは?逆の証明や平行四辺形の問題もわかりやすく解説! 平行線と線分の比 | Ict教材Eboard(イーボード) 「中点連結定理」の. 中線定理の逆が成立するか証明したいのですが…今回高校の . 中線定理の逆が成立するか証明したいのですが… 今回高校の授業で中線定理を復習しました。 すると先生が「この中線定理の逆は成立するかその真偽を調べて証明しろ」 といわれました。 ABC において,BC の中点をMとすると AB^2+AC^2= 2(AM^2+BM^2) これが一般の中線定理です。.